Palancas y herramientas: máquinas simples, ventaja mecánica, tipos y ejemplos de palancas

Es difícil imaginar una herramienta de mano que no brinde ventaja mecánica. Ciertos útiles son en sí mismos palancas. Otros incluyen partes que actúan como palancas. Y el propio cuerpo de quien las usa, además de aplicar la fuerza, sirve a veces como punto de apoyo.

Dada la importancia de las herramientas en el día a día, me propongo reflexionar sobre el asunto, con ayuda del lector. Así pues, en este artículo veremos qué es una palanca, los tres tipos de palancas y ejemplos de ellas. ¿Otro tema tratado? La relación de las palancas con la velocidad, la fuerza y el desplazamiento.

¿Qué es una palanca? Definición de ventaja mecánica

He aquí una definición sencilla de palanca:¹

palanca. Barra rígida capaz de girar sobre un punto de apoyo fijo llamado fulcro.

Que la barra sea rígida es capital. ¿Pues qué valor tendría un martillo de uña a la hora de sacar clavos si su mango fuese flexible? De igual manera, es crucial que el punto de apoyo sea fijo. ¿O acaso es posible mover una piedra con una barreta de hierro apoyando esta en barro?

La palanca, por otra parte, es una de las seis máquinas simples.² Son las restantes el torno, la polea, la cuña, el tornillo y el plano inclinado.³ Lo que hermana las máquinas simples es que todas ellas vencen una fuerza mediante la aplicación de otra.

Así, se define como ventaja mecánica la relación entre la fuerza aplicada (esfuerzo o potencia) y la fuerza resultante (carga o resistencia).

Tipos de palancas

Sobre la barra rígida actúan tres elementos: las dos fuerzas y el fulcro.⁴ La posición central solo puede ocuparla uno de ellos; por lo tanto, solo existen tres tipos de palancas. Las llamamos palancas de primer, segundo y tercer grado.

Palanca de primer grado

En la palanca de primer grado el fulcro está entre el esfuerzo y la resistencia. Ambas fuerzas actúan en la misma dirección. Más adelante veremos qué herramientas sacan provecho de este tipo de palanca. Por el momento, pongamos de ejemplo el subibaja:

Al observar un balancín vemos, en efecto, que las dos fuerzas actúan hacia el terreno. La distancia entre cada una de las fuerzas y el eje de rotación (es decir, el fulcro) se llama brazo. La palanca de primer grado de la Figura 1 está en equilibrio porque ambas fuerzas son iguales y porque sus dos brazos miden lo mismo.

Pero ¿qué pasa si movemos el tronco hacia la izquierda? Si el fulcro pierde el centro, un brazo de la palanca será más largo que el otro. Antes se dijo que la ventaja mecánica en una palanca era la relación entre fuerzas. Pues bien, como vamos a ver, la ventaja mecánica depende de las medidas del brazo de resistencia y el brazo de potencia.

De esta manera, al desplazar el fulcro de la Figura 1 a la izquierda, el niño sentado a la derecha baja (porque gana ventaja mecánica). Pero si un niño menos pesado ocupa su lugar, el subibaja recupera el equilibro (Figura 2).

Palanca de segundo grado

Pero volvamos a los tipos de palanca. En la palanca de segundo grado la resistencia (R) está entre el fulcro (F) y el esfuerzo, también llamado potencia (P). Un ejemplo de ello es la siguiente grapadora:

Al revés que en la anterior, en la palanca de segundo grado las fuerzas actúan en sentidos opuestos. Además, el esfuerzo recorre más distancia que la carga y es menor que ella.

¿Y por qué ocurre esto último? Pues porque el brazo de potencia siempre es más largo que el brazo de resistencia. Algo inevitable, en efecto, al estar la resistencia entre el fulcro y la potencia.

Palanca de tercer grado

Por último, tenemos la palanca de tercer grado. El fulcro en este caso también está en un extremo de la barra, pero la situada en el centro es la potencia.

En una palanca de tercer grado las fuerzas también actúan en sentidos opuestos, como en el caso anterior. Sin embargo, como el brazo de potencia es más corto, el esfuerzo es mayor que la carga. Es decir: la pinza de una cubitera de hielo es más cosa de higiene que de fuerza. Hablaremos de ello más adelante.

Ejemplos de palancas en las herramientas

Lo prometido es deuda. Para entender mejor las ideas y conceptos relacionados con las palancas en las herramientas, vamos a ilustrar el tema con varios ejemplos.

Horquilla para demoler y levantar suelos

Usada para levantar suelos de madera y desmontar tablas de palés, la horquilla de demoler es un claro ejemplo de palanca de primer grado:

El fulcro, en la parte curva del utensilio, permite que la palanca rote. En consecuencia, la herramienta multiplica la fuerza aplicada a la barra y la lleva hasta los dientes, que se levantan para vencer la resistencia.

Comparten dicho patrón buena parte de las herramientas de sacar clavos. Pero vamos con un ejemplo de palanca de primer grado muy diferente...

Alicates de corte

Tijeras, mordazas de presión, tenazas y alicates forman una gran familia de herramientas de corte y sujeción. El que aparece bajo este párrafo, por ejemplo, es un alicate de corte diagonal. Este instrumento, como sus hermanos, se considera una palanca de primer grado.

Como la palanqueta, el alicate tiene un fulcro bien definido que hace las veces de eje de rotación. Sin embargo, esta herramienta no presenta una barra rígida capaz de girar sobre un punto de apoyo fijo, sino dos. Así como la tijera posee dos hojas afiladas, el alicate tiene una pareja de mordazas de corte.

Del largo de dichas bocas y, más importante, de la medida de sus brazos depende la ventaja mecánica del alicate. Por supuesto, en la capacidad de corte del útil también influye, y mucho, la dureza del acero... ¡pero esos son otros lópez!

Ahora bien: ¿cómo funciona un alicate? Si lo miramos de cerca, vemos que cada palanca consta de mordaza y mango. Además, debido a su posición, estas partes se mueven como la barra del subibaja. Si una sube, la otra baja. Y viceversa. Como siempre, hay excepciones (por ejemplo, los alicates para circlips exteriores, que abren al cerrar). Pero esta es la norma general.

Así las cosas, la resistencia (esto es, el cable o alambre) desarrolla una fuerza de igual sentido que la aplicada al mango. Esta fuerza se opone al movimiento de la boca. Sin embargo, la ley de equilibrio de la palanca —que enseguida conoceremos— dice que la fuerza aplicada por su brazo es igual que la carga por el suyo. De resultas, el cable se divide por no soportar la acción de corte de las mordazas.

Hay que poner de relieve, eso sí, que en relación con el desplazamiento de los brazos, las bocas del alicate apenas se mueven. ¡Y esta es la clave! De hecho, se explota al máximo este diseño en herramientas muy potentes, como las cizallas de cortar varillas.

En suma, cuanto más largos los brazos de una herramienta, mayor su capacidad de corte.

Llegados a este punto, podríamos buscar muchas más palancas de primer grado... Pero ¿no va siendo hora de hacer experimentos? Por ejemplo, ¿qué pasará al intercambiar la posición del fulcro y la resistencia? ¡Vamos entonces con la carretilla!

Carretilla

La carretilla es un vivo ejemplo de palanca de segundo grado. La rueda es el fulcro; la cuba es la resistencia; los mangos, la potencia.

Pero ¿se gana ventaja mecánica con la carretilla? Sin duda. Por ser palanca de segundo grado, la medida del brazo de potencia (es decir, desde el centro de la rueda a los mangos) es mayor que la del brazo de resistencia (del centro de la rueda al punto medio de la cuba).

A simple vista se puede comprobar que al levantar los mangos de la carretilla la separación entre estos y el terreno aumenta más que la distancia existente entre las patas y este. En efecto: la carretilla es una máquina multiplicadora de fuerza. Lo son todas las palancas de segundo grado.

Pero, sin presión de aire suficiente, la rueda neumática de la carretilla no transportará muy lejos la carga. Por suerte, la bomba neumática de pie es otro ejemplo de palanca de segundo grado...

Bomba neumática de pie

En la carretilla, el esfuerzo se aplica hacia arriba para vencer la gravedad. Las fuerzas en la bomba de pie también se oponen. Porque se ha de presionar el pedal para contrarrestar la resistencia de los muelles y los émbolos de los cilindros. Así es como se bombea aire.

Dos ejemplos clásicos de palancas de segundo grado son el cascanueces y el abrebotellas. Pero vale la pena descubrir un instrumento más versátil. Uno que combina dos tipos de palancas...

Tenaza de electricista multiusos

La siguiente tenaza de electricista multiusos presenta funciones a la izquierda y a la derecha del fulcro:

Al usar el Drahtschneider de la punta, o 'cortador de cables', la herramienta actúa como palanca de primer grado. Pero ¿y al utilizar el 'pelador calibrado' o Abisolierung para los amigos? ¡Bingo! Palanca de segundo grado. Y lo mismo ocurre al cortar tornillos o crimpar punteras huecas: la resistencia se ubica entre el eje de rotación y la potencia.

Nuestra siguiente parada: intercambiar las posiciones de la potencia y la resistencia. Pero sin tocar el punto de apoyo.

Martillo

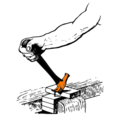
¿Qué herramientas son palancas de tercer grado? Por ejemplo, la maceta. También lo son los martillos, incluido el de orejas —siempre que se use para golpear (y no para sacar clavos)—.

Pero ¡un momento! ¿Cuál es el fulcro del martillo? Aquí hay truco. Como en tantas otras herramientas con palancas de tercer grado, el punto de apoyo hay que buscarlo en el cuerpo humano... En el caso del martillo, el fulcro puede ser la muñeca o el codo.

La resistencia es el objeto que se martillea. La mano aplica la fuerza entre la cabeza del martillo y el punto de apoyo. Resistencia, potencia y fulcro. Por este orden. En consecuencia, palanca de tercer grado. Así es.

En este tipo de palanca, al revés que en la de segundo grado, el brazo largo es el de resistencia. Por tanto, aunque suene absurdo, el esfuerzo es mayor que la potencia. De hecho, esto es fácil de comprobar:

• al coger el mango cerca de la cabeza se pierde fuerza, pero se controla mejor el martillo
• al coger el mango por su extremo, se pierde control, pero aumenta la fuerza transmitida a la cabeza

Todo ello es relativo. Porque un martillo debe estar balanceado para resultar cómodo. Ahora bien: en el segundo caso es claro que cuanto más largo sea el mango, más cuesta manejar el martillo.

Un ejemplo evidente es la almádena. Se requiere mucha fuerza para sostener en horizontal una maza de 5 kg tomándola con una sola mano por el final del mango. No digamos ya para usarla... ¡Ni siquiera Sansón hubiera podido con ella!

Rastrillo

Cambiando de oficio, el rastrillo de jardín es una herramienta mucho más ligera. ¡Qué alivio! Bueno, o no tanto. Porque rastrillar hojas, de igual forma, es tarea que exige usar ambas manos.

En efecto, el rastrillo es otro ejemplo de palanca de tercer grado. Una mano hace de fulcro; la otra aplica el esfuerzo y las hojas se resisten a ser barridas. Como en el escenario anterior, estamos ante una herramienta reductora de fuerza.

¿Y cuál es el beneficio de tal desventaja mecánica? Si la carretilla sacrificaba distancia por fuerza, el rastrillo canjea fuerza por distancia. Así, poco desplazamiento en las manos se traduce en muchas hojas recogidas.

En todo caso, sin importar el tipo de palanca, la ley de la palanca siempre se cumple.

La ley de la palanca

La palanca no es un invento reciente. Sobra decirlo. De hecho, data de la época prehistórica.

En sellos cilíndricos de Mesopotamia del tercer milenio a. C. ya aparece documentado el uso del cigoñal o shaduf para sacar agua de ríos. Se trata de una máquina simple usada a modo de palanca, también llamada cigüeñal o bimbalete.

Así que Arquímedes no inventó la palanca (s. iii a. C.). Pero sí explicó el principio de la palanca. Aparte de la célebre cita Dadme un punto de apoyo y movére el mundo, el ingeniero y filósofo griego dejó escrita la siguiente explicación de la ley de la palanca:

Las magnitudes están en equilibrio a distancias recíprocamente proporcionales a sus pesos. Arquímedes.

La ley de la palanca nos dice que la potencia por su brazo es igual a la resistencia por el suyo. Es decir: potencia × brazo de potencia = resistencia × brazo de resistencia. Lo que de forma matemática se expresa así:

P × Bp = R × Br

Por otro lado, la ventaja mecánica equivale a la relación entre la resistencia y la potencia:

VM = R / P

En consecuencia, si se manipula la primera ecuación y se sustituye R / P en la segunda:

VM = Br / Bp

En otras palabras, la ventaja mecánica de la palanca establece la relación entre la fuerza de salida y la de entrada (resistencia / potencia).

Ventaja mecánica en cada tipo de palanca

La palanca de primer grado puede actuar como multiplicador o reductor de fuerza según su ventaja mecánica. Si sus dos brazos son iguales, la relación de fuerzas no se modifica. Sí lo hará, en todos los casos, la dirección de las fuerzas. Esto se ve mejor en herramientas como la palanqueta, pero también se da en alicates, tijeras, etc.

En cambio, las palancas de segundo y de tercer grado son, respectivamente, máquinas multiplicadoras y reductoras de fuerza. Ninguna de ellas altera la dirección de las fuerzas.

Los escenarios posibles se resumen en la siguiente tabla:

La fuerza se multiplica en detrimento del desplazamiento. Y viceversa. La moraleja es que ningún tipo de palanca multiplica al mismo tiempo la fuerza y el desplazamiento (o la velocidad).

Ahora sí: nos sabemos la cartilla. Pero no habremos sacado nada en claro sin una forma de recordar el asunto. Al rescate llega una útil regla mnemotécnica sobre los tipos de palancas...

Una regla mnemotécnica para recordar los tipos de palanca

¿Cuál era cual? Es fácil olvidarse de los tipos de palanca. Pero un código sencillo te ayudará a recordarlo: 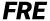. Si olvidas el asunto con FREcuencia o sabes que te van a FREír a preguntas sobre el tema, he aquí la palabra mágica: FRE: Fulcro, Resistencia, Esfuerzo.

La cosa va así. Cada letra y su lugar en la sigla (en número) representan la posición central del elemento en cada tipo de palanca:

• Si es el (F)ulcro, palanca de primer grado (1).
• Si es la (R)esistencia, palanca de segundo grado (2).
• Si es el (E)sfuerzo o potencia, palanca de tercer grado (3).

Para recordar la regla en sí, piensa en algo gráfico. Por ejemplo, imagina a FREddy Krueger persiguiéndote con una FREgona —palanca de tercer grado, por cierto—.

Nota: esta regla mnemotécnica es una adaptación de la idea original que aparece en este vídeo (en inglés) del blog MooMooMath.

Otro vídeo recomendado sobre los tipos de palancas es el siguiente:

Colofón y resumen

¿En qué parte de la boca del alicate se pone el alambre para cortarlo con el menor esfuerzo posible? Nos interesa acortar el brazo de resistencia... Luego lo más cerca posible del eje.

Se aplica el mismo principio en tijeras y cizallas. No así en tenazas de corte, pues la distancia de sus filos frontales al punto de apoyo es fija. Solo cabe entonces alargar el brazo de potencia, esto es, cogerlas por el final de los mangos.

En suma, saber cómo funciona una palanca te ayuda a sacar el máximo partido de tus herramientas.

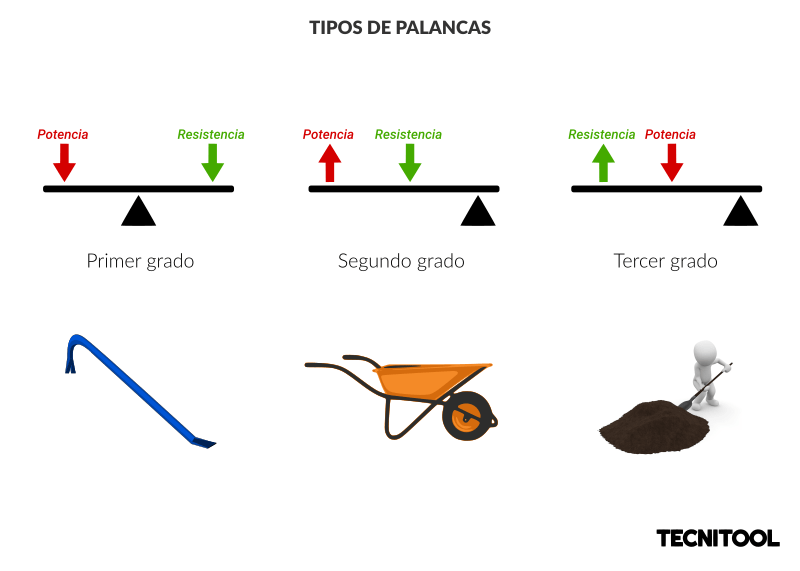
A modo de resumen, la palanca es la barra rígida que gira alrededor de un fulcro y sobre la que actúan dos fuerzas: resistencia y potencia. Puesto que solo uno de estos elementos puede ocupar el lugar central, solo hay tres tipos de palancas, respectivamente, de primer, segundo y tercer grado.